例えば1/100の確率の台があるとすると、100回スタートすると必ず大当りが1回出ると思ってしまいがちですが、そのようなことにはなりません。この確率は、常に確率が1/100であることを表していて、朝一番の1回目のスタートも、300回大当りが出なかった301回目のスタートも、時短が終わった後のスタートもすべて同じ1/100ということになります。つまり、100回スタートしても必ず大当りが1回出るというものではないということになります。

サイコロを例に出すと、サイコロを振ったときに1の出る確率は1/6です。6回振ったら必ず1回1が出るわけではなく、6回振ったら、1が3回出ることもあれば、1回も出ないことがあります。パチンコの確率も同じような考え方となっています。
パチンコの場合は、サイコロではなく機械の中にあるプログラムで抽選が行われています。その抽選は、スタートチャッカーに玉が入った時に行われ、その抽選結果によってリーチアクションなどの画面が表示されています。
朝一番で10回目のスタートで大当りすればその時の確率は1/10、次に300回スタートして大当りすれば、その時は1/300の確率というふうに、100回ちょうどで大当りになることは極めてマレなことです。しかし、1/100の確率の機種であれば、大当り回数が多くなれば、どこかで平均確率が1/100になるのではないか?だから1/100と書いてあるのではないか?という疑問が出てきます。
そこで、もっと確率の低いサイコロで実験してみました。サイコロの目の出る確率1/6は、どのくらい振れば1/6に近づくのだろう?実際にサイコロを、2,000回振ってみてどうなったかの結果です。
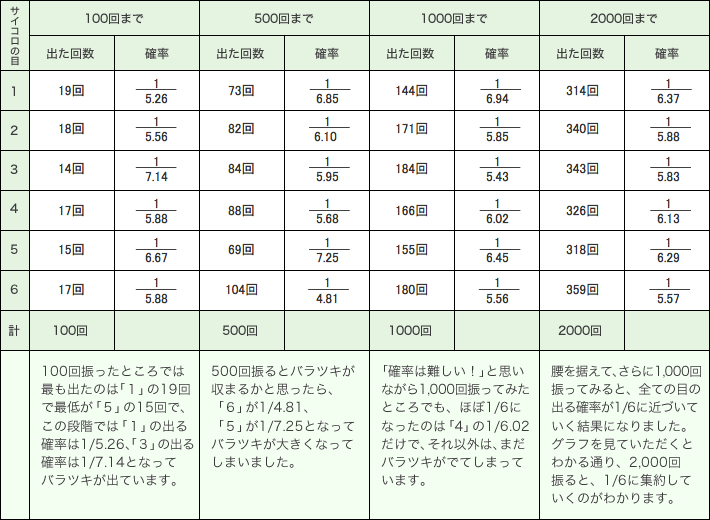
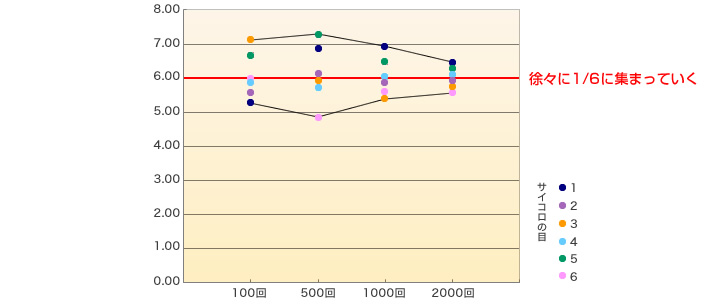
サイコロと同じように、スタート回数が多くなれば、1/100に近づくはずですが、どのくらいスタートさせれば近づくのかを統計学を用いて、計算してみます。
それぞれの500回を「1セット」と言うとすると、500回を4セット実施したなかで、 500回スタートして1/100となったのは1セットありますので、1/4=25%の確度となります。
もし、1/83も1/100の誤差の範囲(誤差20%)とした場合は、2セットありましたので、2/4=50%の確度となります。



この回数を増やしていって、誤差5%(1/95~1/106の範囲)で確度90%(セット数の90%)となるには、1セットを約11万回(107,140回)のスタートにする必要があります。
統計上は、こんなにスタートしないと、確率は近くなっていかない計算になります。
1つの店舗に100台の1/100の機種があるとした場合、そのうちの90台の平均大当り確率が1/96~1/106の範囲となるには、100台それぞれが約10万回スタートしなければならないことになります。
1/100の機種の合計スタート回数が約11万回ある店舗が100店舗あったとすると、そのうち90店舗は、平均大当り確率が1/96~1/106に入るということになります。
もっと精度を上げるとどうなるかというと、誤差1%(1/99~1/101の範囲)で、確度99%とすると、約657万回のスタートが必要となります。
この数字はあくまで統計上の数字なので、実際のパチンコとは異なる場合もあるかもしれません。統計上のことだけでなく、経験や勘で台を選んだり、運もフル活用してパチンコを楽しんでいただければと思います。
※確率誤差、確度によるスタート回転数の算出は、正規分布の確率密度関数を用いて計算しています。
